From Chemistry to Calculus

October 17, 2024

Introduction

⊕From YouTube The Math Sorcerer.

As mentioned in my blog, the study of Chemical Principles by Atkin inspired my study of Calculus. I tried choosing a book, and this time some parts of the internet pointed me to a very nice book—Calculus by James Stewart.

From the study of first-year general chemistry, I saw that calculus was the fundamental of a lot of natural sciences in general—specifically, more sophisticated studies of the natural world required more sophisticated math, the kind of math that involves meaningful discussions and calculations about infinitesimals and infinities.

⊕Neither subject is monotone building-up or breaking-down, but generally speaking, one type of thinking dominates over the other.

Calculus is a completely different challenge: it is more abstract, less (but still) algorithmic, and the techniques are more dependent upon each other, generally speaking, than chemistry. Chemistry uses a breaking-down principle in understanding the real world, and calculus uses a building-up principle in deriving mathematical techniques from previously acquired skills and intuitions.

Lessons from Chemistry

⊕
127 cards in total were made.

The most important lesson I learned from Chemistry is that in order to retain information, spaced repetition is absolutely necessary. For each discrete skill or algorithm, I would choose a step, formula, or approach that best reminds me of its entirety. I would then make flashcards, sometimes bidirectionally, with MathJax notation on Anki.

Surprisingly, I did not need to use any external resources, apart from (god forbid) Chegg to access some of the more detailed and fleshed-out answers to some of the harder problems. A well-written solution is usually enough for me to understand what I was supposed to do. If I had more time, I would utilize some open-source college-level course recordings, but this did not prove to be necessary.

However, one crucial change is to base my daily tasks on time spent at work, and not sections or exercises completed. This decreased my stress, because when I was working on chemistry I sometimes had to work “overtime” to complete a particularly long chapter or section. It also encourages focus, consistent effort, and habit-building: after a month, I found myself consciously finding time for math study. I believe this focused mental exercise has served me well in a this hectic and always-busy world.

⊕
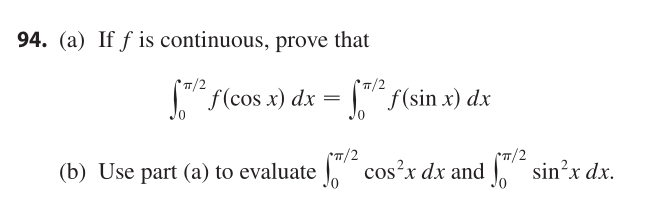
94 problems in a single section and this is typical.

Additionally, Stewart’s book had an absolute abundance of exercises. I did not find it to be necessary to complete every single one—not even every odd-numbered exercise. Some exercises are extremely repetitive and are obviously used better under an instructor’s discretion. The trick for me is to find a clear ascending progression in difficulty and abstraction. I chose to work on all of the exercises on the “atlas” of the progression, which proved to be reasonably effective.

⊕
Problem Plus usually requires a more creative solution.

I chose to not utilize the Problems Plus section of the book, but after I did some problems after I completed the entire book, I think I absolutely should have. These are project-style problems that sometimes model the real world, and they usually serve as excellent challenges for mathematical thinking and the skills practiced in that particular chapter. If you’re like me, someone who loves solving mathematical puzzles, Problems Plus would be an awesome treat for you.

Looking ahead

Unfortunately, this period of study did not enlighten me to any further methods of improvements. I knew that I was mediocre at retaining technical skills and information, I sometimes rejected useful strategies for the pursuit of speed, and I sometimes skip over things that I don’t fully understand. However, as of right now, I don’t have any good methods for fixing any of them apart from “just don’t do it”, which will just take time.

⊕
From UTM by Springer.

However, from the study of math, I have found a greater challenge that may provide me with more insight: the real analysis book Understanding Analysis. It will familiarize me with proofs, provide a rigorous argument for calculus, and serve as an experience with theorem-proof type books. It will be an ambitious endeavor for a high school student, but I am up for the challenge.

I hope more insight to undergraduate-level self-studying will come out of this experience, and maybe a foundation for higher-level math, too.

mi tawa.